1303. Ультрабыстрая сортировка
В этой задаче
Вам следует проанализировать работу конкретного алгоритма сортировки. Алгоритм
обрабатывает последовательность из n
различных целых чисел, меняя местами соседние элементы до тех пор пока все
числа не будут находиться в возрастающем порядке. Например, для
последовательности
9 1 0 5 4
результатом
ультрабыстрой сортировки будет
0 1 4 5 9
Вам необходимо
установить наименьшее количество перестановок соседних элементов, необходимое
для расположения всех элементов последовательности
в возрастающем порядке.
Вход. Состоит из нескольких тестов. Первая строка каждого теста
содержит длину входной последовательности n
(n ≤ 500,000). Каждая из
следующих n строк содержит одно целое
число ai (0 ≤ ai ≤ 999999999) - i-ый элемент последовательности.
Последний тест содержит n = 0 и не
обрабатывается.
Выход. Для каждой
входной последовательности в отдельной строке вывести целое число op – наименьшее количество перестановок
соседних элементов, необходимое для сортировки элементов последовательности.
|
Пример
входа |
Пример
выхода |
|
5 9 1 0 5 4 3 1 2 3 0 |
6 0 |
РЕШЕНИЕ
сортировка
слиянием
Анализ алгоритма
Наименьшее
количество перестановок соседних элементов, необходимое для упорядочивания
элементов последовательности, равно количеству инверсий во входной
последовательности. Искомое число инверсий можно найти за время O(nlog2n), промоделировав сортировку слиянием (merge sort).
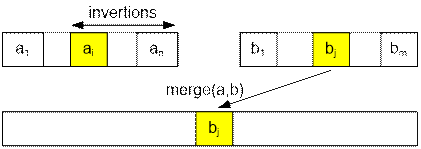
Рассмотрим
слияние двух отсортированных массивов A = (a1,
…, an) и B = (b1, …, bm). Пусть уже слиты части A = (a1, …, ai-1)
и B = (b1, …, bj-1), и в текущий
момент сравниваются значения ai
и bj. Пусть оказывается ai > bj и элемент bj
переносится в сливаемый массив. Тогда утверждается, что bj образует инверсии только с элементами ai, …, an, и таких инверсий имеется в точности n – i
+ 1.
Пример
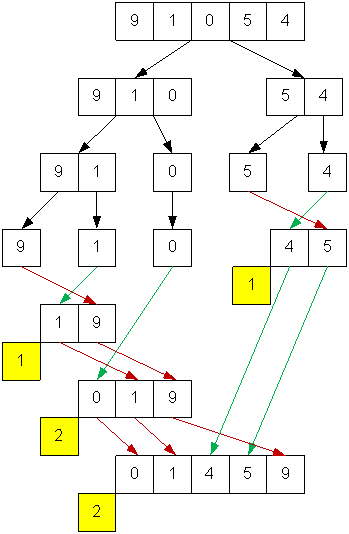
Посчитаем инверсии в первом и во втором примере.

Рассмотрим
сортировку слиянием на первом примере. Инверсии подсчитываются на этапе слияния
последовательностей. Около каждой последовательности, полученной в результате
слияния, записано количество инверсий, которое образуют элементы сливаемых
последовательностей.
Реализация алгоритма
Входную последовательность будем
хранить в массиве m.
int *m;
Слияние
отсортированных массивов a[bL] ... a[bR] и a[cL] ... a[cR] в a[bL] ... a[cR]. Отметим, что у нас всегда bR + 1 = cL. Для слияния используем дополнительный массив res.
void merge(int
*a, int bL, int
bR, int cL, int
cR)
{
Занесем в len количество сливаемых элементов. Создадим массив res (буфер), в
который будут сливаться элементы.
int i = 0,
Left = bL, len = cR - bL + 1;
int *res = new int[len];
Текущей просматриваемой позицией в
первой последовательности является bL, во
второй cL. То есть на каждой итерации
сравниваются a[bL] и a[cL]. Меньшее из этих значений
заносится в буфер res. По мере добавленияя элементов в буфер значения bL и cL увеличиваются на 1. Как только одно из них дойдет до конца
последовательности (bL станет
больше bR или cL станет больше cR), цикл
заканчивается. Это означает, что элементы одной из сливаемых
последовательностей уже полностью перенесены в буфер.
Количество инверсий swaps изменяется при перенесении
элемента второй последовательности в буфер. При этом swaps увеличивается на число еще неслитых элементов первой
последовательности, равное bR – bL + 1 (из первой последовательности
еще не перенесены в буфер элементы a[bL .. bR]).
while((bL
<= bR) && (cL <= cR))
if (a[bL]
<= a[cL]) res[i++] = a[bL++];
else res[i++] =
a[cL++], swaps += bR - bL + 1;
Одна из сливаемых последовательностей
закончилась. Следует скопировать в конец буфера остаток другой
последовательности.
while (bL
<= bR) res[i++] = a[bL++];
while (cL
<= cR) res[i++] = a[cL++];
Копируем все содержимое буфера в
массив а, начиная с ячейки Left.
memcpy(a + Left,res,len*sizeof(int));
Удаляем буфер – весь массив res.
delete[] res;
}
Сортируем массив a[left
... right] методом “разделяй и
властвуй”. Для этого разделим его на две части a[left ... middle] и a[middle + 1 ... right], отсортируем отдельно каждую из них, после чего произведем
слияние.
void mergeSort(int
*a, int left, int
right)
{
if (left
>= right) return;
int middle =
(left + right) / 2;
mergeSort(a,left,middle);
mergeSort(a,middle+1,right);
merge(a, left, middle, middle + 1, right);
}
Основная часть программы. Выделяем
память под входной массив, считываем его и запускаем сортировку слиянием, в
которой подсчитываем количество инверсий swaps.
while(scanf("%d",&n),n)
{
m = new int[n];
for(swaps = i
= 0; i < n; i++) scanf("%d",&m[i]);
mergeSort(m, 0, n - 1);
printf("%lld\n",swaps);
delete[] m;
}
Реализация с использованием
явной сортировки
#include <cstdio>
#include <string>
#include <vector>
#include <algorithm>
#define MAX 500001
using namespace
std;
int m[MAX];
int n, i, j;
long long
swaps;
void merge(int
left, int middle, int
right)
{
int i = left,
j = middle + 1;
while((i
<= middle) && (j <= right))
{
if (m[i]
<= m[j])
i++;
else
{
j++;
swaps += middle - i + 1;
}
}
sort(m + left, m + right + 1);
}
void mergeSort(int
left, int right)
{
if (left <
right)
{
int middle
= (left + right) / 2;
mergeSort(left,middle);
mergeSort(middle+1,right);
merge(left, middle, right);
}
}
int main(void)
{
while(scanf("%d",&n),n)
{
for(swaps =
i = 0; i < n; i++) scanf("%d",&m[i]);
mergeSort(0, n - 1);
printf("%lld\n",swaps);
}
return 0;
}